Welke toon horen we?

[Peter van Velzen]

IK heb nooit beseft wat deze video uitlegt.
(engeks 6 minuten)

[Maria]

Helemaal begrijp ik het ook niet, vooral als één van de trillingen wordt weggelaten en het geheel blijft dezelfde toonhoogte houden.

Wat ik begrepen heb:
Bij samengaan van trillingen van verschillende frequenties ontstaat er door summatie van gelijkvallende pieken een nieuwe duidelijke trilling.
Dat heet interferentie.
De meelopende trillingen van andere frequenties hoor je dan niet als een bepaalde toonhoogte, maar als toonkleur of klankkleur.

En dit niet alleen veroorzaakt door het instrument, maar ook mede gevormd door absorbering en weerkaatsing van de verschillende trillingen door de omgeving, totdat het ons oor bereikt.

Ik kwam dit nog tegen.
https://nl.wikipedia.org/wiki/Zweving#A ... _zwevingen
Ik weet niet of het een echte aanvulling is op deze kwesties, maar maakt wel wat meer duidelijk over geluidsfrequenties en tonen voor de wat meer technici onder ons.
Ook hoorbaar gemaakt.

[axxyanus]

Helemaal begrijp ik het ook niet, vooral als één van de trillingen wordt weggelaten en het geheel blijft dezelfde toonhoogte houden.

Het heeft te maken met periodieke functies. Wat je daarbij in het oog moet houden is dat de periode omgekeerd evenredig is aan de frequentie.

Dus nemen we twee functies F₁ en F₂. F₁ heeft een periode van 4 en F₂ heeft een periode van 6.
We hebben dus de volgende vergelijkingen:

• F₁(x) = F₁(x + 4n)
• F₂(x) = F₂(x + 6k)

En om het wat eenvoudig te houden hebben we de volgende frequenties f₁ = 2400/4 = 600 en f₂ = 2400/6 = 400.

Wat gebeurt er nu als we deze functies optellen. F_s = F₁ + F₂

F_s(x) = F₁(x) + F₂(x) = F₁(x + 4n) + F₂(x + 6k) = F₁(x + 12) + F₂(x + 12)

We hebben dus nu een functie met periode 12 en dus als frequentie: f_s = 2400/12 = 200.

Dus als we twee periodieke functie bij elkaar optellen, dan krijgen we een functie met als periode het kleinste gemeen veelvoud van de oorspronkelijke periodes en omdat frequenctie het omgekeerde zijn van periodes, krijgen we daardoor een functie met als frequenctie (iets dat evenredig is met) de grootste gemene deler van de oorspronkelijke frequenties.

[Maria]

Helemaal begrijp ik het ook niet, vooral als één van de trillingen wordt weggelaten en het geheel blijft dezelfde toonhoogte houden.

Het heeft te maken met periodieke functies. Wat je daarbij in het oog moet houden is dat de periode omgekeerd evenredig is aan de frequentie.

Zoiets dus.
Ik kon het alleen niet vatten en verwoorden.
Ik heb wel wat over tonen en muziek geleerd, maar het wiskundige deel bleef wat begrip betreft achter.

[Bonjour]

Maria, stel je eens een waterbak voor met 2 plekken waar golven gemaakt worden. We deden dit vroeger bij natuurkunde met een plexiglas bak die op de overheadprojector geplaatst werd. (Probeer dit experiment nog maar eens met die digischermen die nu in de klaslokalen hangen). Als de 2 plekken met dezelfde frequentie bewegen krijg je een interferentie patroon. Er zijn plekken waar het water stil blijft staan. In de klas hield het experiment nu ongeveer op.
We gaan verder. We draaien de voeding(elektriciteits)draadjes om van een van de bewegers, zodat ie juist naar achter gaat op het moment dat ie eerder naar voren ging. Natuurkundig heet dit dat de fase 180 graden gedraaid is. Het interferentie patroon wijzigt nu in de glasbak. Precies de plekken die eerder stilstonden bewegen nu en vice versa.

En nu maken we het nog iets ingewikkelder. We pakken een aparte sinusgenerator voor die beweger en zetten daar een iets andere frequentie op. Op het moment dat beide bewegers synchroon gaan, zal je het interferentie patroon zien zoals in het eerste experiment, maar even later als de bewegers in tegengestelde beweging gaan, zie je juist het interferentie patroon van het 2de experiment. Het interferentiepatroon wisselt dus steeds. Elke plek in de bak krijgt 2 sinussen van iets verschillende frequentie en die doven elkaar dus steeds een tijdje uit en versterken elkaar daarna weer een tijdje. Net afhankelijk van de fase waar elke sinus in zit. Ik heb er zelf een plaatje van gevonden. Rood en blauw zijn de verschillende sinussen en geel de optelsom ervan.

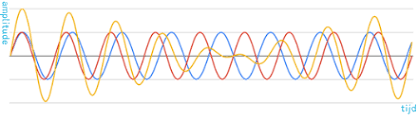
De frequentie waarin zich dit herhaalt is het verschil van de frequenties. Daar zit de wiskunde van Axxyanus. (Dank. Hoef ik die niet te doen.)
In het geluid merk je dit bijvoorbeeld als gitaarsnaren gestemd worden. Zolang ze niet precies dezelfde frequentie hebben, hoor je een zweving. En als het verschil nog groter wordt ervoor je die zweving als een nieuwe toon.

Wat de video mooi uitlegt is hoe de harmonischen de klank van een instrument bepalen, terwijl de basisfrequentie gelijk is.

[Maria]

Wat de video mooi uitlegt is hoe de harmonischen de klank van een instrument bepalen, terwijl de basisfrequentie gelijk is.

Het principe van interferentie ken ik en heb er ook mee gewerkt.
Ik beschreef dat ook al in mijn reactie.
Alleen nooit met de wiskundige formules, zoals ik ook al aanreikte in het Wikipedia artikel.

Nu zie ik hierin dat het geen aanvulling is op de eigenlijke vraag.
Waar het mij om ging is het stukje "The missing fundamental".

Helemaal begrijp ik het ook niet, vooral als één van de trillingen wordt weggelaten en het geheel blijft dezelfde toonhoogte houden.

https://nl.wikipedia.org/wiki/Zweving#A ... _zwevingen
Ik weet niet of het een echte aanvulling is op deze kwesties, maar maakt wel wat meer duidelijk over geluidsfrequenties en tonen voor de wat meer technici onder ons.

Dus als er later, als de zuivere toon al gevormd uit de verschillende frequenties en een belangrijke frequentie wordt weggelaten, toch de oorspronkelijke frequentie, dus toonhoogte doorgang vindt.
Maar misschien is mijn Engels niet voldoende en begrijp ik verkeerd wat er wordt gesteld.
Ik vermoedde, dat het Peter ook daarom ging.
Maar hij heeft nog niet gereageerd.

[axxyanus]

Dus als er later, als de zuivere toon al gevormd uit de verschillende frequenties en een belangrijke frequentie wordt weggelaten, toch de oorspronkelijke frequentie, dus toonhoogte doorgang vindt.

Stel dat je drie frequenties combineert 200Hz (Periode 12), 400Hz(Periode 6) en 600Hz(Periode 4). Dan is de periode van deze combinatie het kleinst gemene veelvoud van de drie. Dat is in dit geval dus een periode van 12 met een frequentie van 200Hz. Dat komt dus omdat de andere frequenties veelvouden zijn van deze frequentie of omdat de andere periodes, deelbaar zijn door deze periode.

Als je nu de eerste toon weglaat, dus die van 200Hz of periode 12, dan blijft de periode van de overblijvende combinatie 12 (want het kleinst gemeen veelvoud van 6 en 4 is 12) en de frequentie van de combinatie blijft dus ook 200Hz. Dat is wat met de "missing fundamental" bedoeld wordt. De periode (en ferquentie) van een combinatie die verschilt van alle gebruikte componenten.

[heeck]

Deze hoort bij het spelen met tonen:



Roeland

[Maria]

Stel dat je drie frequenties combineert 200Hz (Periode 12), 400Hz(Periode 6) en 600Hz(Periode 4). Dan is de periode van deze combinatie het kleinst gemene veelvoud van de drie. Dat is in dit geval dus een periode van 12 met een frequentie van 200Hz. Dat komt dus omdat de andere frequenties veelvouden zijn van deze frequentie of omdat de andere periodes, deelbaar zijn door deze periode.

Dank.
Bij veelvouden is dat idd. ook logisch.

[heeck]

Hele kleine luidsprekers die te klein zijn voor de grotere golflengtes kunnen toch de lage klank geven door naast technische vondsten ook bloedslim die missende grondtoon in te zetten. *)

Omgekeerd kan je zelf ook:


Oefenen gaat het best in de badkamer met je gezicht naar de muur op ongeveer 20-40 cm afstand.

Roeland

*)
https://www.compadre.org/osp/EJSS/4488/273.htm